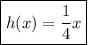Answer:

Explanation:
The inverse of a function is its reflection in the line y = x.
Given function:
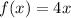
The given function has an unrestricted domain and range.
- Domain: (-∞, ∞) → all real numbers.
- Range: (-∞, ∞) → all real numbers.
To find the inverse of the given function, first replace f(x) with y:
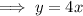
Rearrange the equation to isolate x:
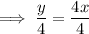
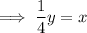
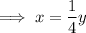
Swap the x for f⁻¹(x) and the y for x:
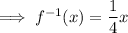
This is the inverse of the given function.
The domain of the inverse function is the range of the function.
The range of the inverse function is the domain of the function.
Therefore, the domain and the range of the inverse function are unrestricted.
- Domain: (-∞, ∞) → all real numbers
- Range: (-∞, ∞) → all real numbers
Therefore, the function that represents the inverse of f(x) = 4x is: