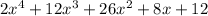Answer:
Choice A:
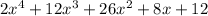
Explanation:
This can be done without computing the entire product and difference with a little bit of thought. If you look at the answer choices they have different values for the coefficient of
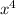 Choices B and C do not even have a term for
Choices B and C do not even have a term for
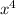
So if we focus on only the part of the multiplication which will produce an
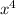 term we can find the right choice
term we can find the right choice
The area of Shape A is (3x² + 2)(7x² + 4x + 8)
One of the terms arises from 3x² x 7x² =
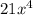
The area of Shape B = (3x²+2)(3x^2+2)
So the
Look at the answer choices.
The first component has x term
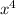 which is obtained by multiplying
which is obtained by multiplying
(3x²)(3x²) =
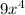
If we subtract the area of Shape B from Shape A , we get the
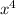 term as
term as
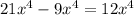
The only choice which has
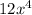 as a term is the first one, Choice A
as a term is the first one, Choice A
So answer is Choice A: