Question

8x^2+16x-4=0

I don't understand I think there are two ways to do it but I'm not sure if one is correct or not.

Answer 1

x = -1 ± (√6)/2

Explanation:

You want the solution to 8x^2+16x-4=0 two ways.

Reducing the equation

We notice all of the coefficients are multiples of 4. This means we can divide that factor out, leaving us with the quadratic ...

2x^2 +4x -1 = 0

Completing the square

One way to solve such a quadratic is by "completing the square." The solutions are found by taking the square root of the square.

2x^2 +4x -1 = 0

2x^2 +4x = 1 . . . . . . . separate the constant from the variable terms

2(x^2 +2x) = 1 . . . . . . factor out the leading coefficient

2(x^2 +2x +1) = 1 +2(1) . . . . . add the square of half the x coefficient

The square is completed at this point.

2(x +1)^2 = 3 . . . . . . . . write the left side as a square, collect terms

(x +1)^2 = 3/2 . . . . . . . . divide by the leading coefficient

x +1 = ±√(3/2) = ±(√6)/2 . . . . . take the square root

x = -1 ± (√6)/2 . . . . . . . subtract 1; the solutions to the equation

Quadratic formula

The reduced equation can be compared to the standard form ...

ax^2 +bx +c = 0

to see that a=2, b=4, c=-1.

The solution to the equation using the quadratic formula is ...

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x=(-4\pm√(4^2-4(2)(-1)))/(2(2))\\\\\boxed{x=-1\pm(√(6))/(2)}`

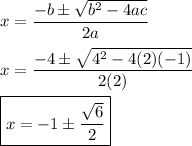
Graph

The attached graph shows the solutions to be approximately -2.225 and +0.225. The vertex (-1, -12) and the leading coefficient (8) tell you these solutions are -1±√(12/8) = -1±(√6)/2.