Answer:
88.9294
Explanation:
So for this problem we need to convert the top 2% into a z-score, which can be done using a calculator. You also first have to convert top 2% into 98% percentile. In doing so you'll approximately get:
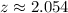
This z-score just represents how many standard deviations away this is from the mean.
So this means that the minimum score would be represented as:
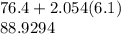
This can be rounded as needed, but this would approximately be the minimum score to be in the top 2%