1. With N = Newtons, m = meters, we have
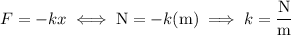
N itself can be broken down according to Newton's second law,
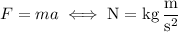
so the dimension of the force
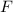 is
is
![[F] = [M\cdot L\cdot T^(-2)]](https://img.qammunity.org/2023/formulas/physics/high-school/twqrmmxxgf3ey39sglbuqfxepts07r2m3b.png)
(where M = mass, L = length, T = time) and hence the dimension of
 is
is
![[k] = \left[(M\cdot L\cdot T^(-2))/(L)\right] = \boxed{[M\cdot T^(-2)]}](https://img.qammunity.org/2023/formulas/physics/high-school/j04on5wzxcnoo0hfl38t690k3gudpig5n1.png)
2.
a. With N = Newtons, A = amperes, and m = meters,

b. The dimension of
 is
is
![[k] = \left[((M\cdot L\cdot T^(-2))\cdot L)/(I^2)\right] = \boxed{[M\cdotL^2\cdot T^(-2)\cdot I^(-2)]}](https://img.qammunity.org/2023/formulas/physics/high-school/t9xsbf6z3t36br68xcmbd7cbu14jskh38e.png)
(where I = current, with "I" as in capital i)