Question

If the hypotenus of a right triangle is 6 m and one side is 4 m, what's the length of the other side

Answer 1

`√(20) \text{ or } 2√(5)`

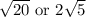
Explanation:

So in this question we want to use the Pythagorean Theorem which essentially gives us a relationship between the sides of a triangle and is as follows:
`a^2+b^2=c^2`

In this formula the "a" and "b" represent the base and the height and "c" represents the hypotenuse of the triangle

The order in which you assign "a" and "b" do not matter, so let's just say that:
`a=4\ \text{and}\ c=6`

Although it is important that you assign the hypotenuse to "c".

So plugging in known values we have the equation:

`4^2 +b^2=6^2`

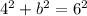
Square the values

`16+b^2=36`

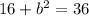
Subtract1 16 from both sides

`b^2=20`

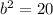
take the square root of both sides

`b=√(20)`

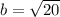
This "b" represents our other side, which we did not initially know, so this is our answer :)

You can simplify this further by separating the radical into:
`√(20) = √(4) * √(5) = 2√(5)`