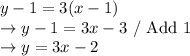Answer:
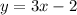
Explanation:
Step 1) Find two points from the graph to work with
I would personally use the points (0, -2) and (1, 1) as they are the most comfortable to work with from the given graph.
Step 2) Find the slope
A function's slope is given by the formula:
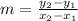
We can now substitute the coordinates of the points we found in Step 1 in the formula to find the function's slope.
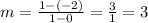
Step 3) Find the line's equation
Finally, we can substitute the slope we found in Step 2, as well as one of the points we found in Step 1, into the formula
 to find the line's equation.
to find the line's equation.