Answer:
y = 1x + 5
Explanation:
First, lets calculate the equation of the line passing through (5, 7) and (1, 3) in slope-intercept form
The general equation of a line in slope-intercept form is
y = mx + b
where m = slope and b = y-intercept is rise over run =
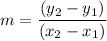
where (x₁, y₁) and (x₂, y₂) are any two points on the line
For the line passing through (5, 7) and (1, 3) , the slope
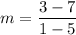
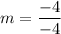
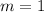
To compute the y-intercept, plug in any of the two points x and y values and solve for b
Take point 5, 7 ==> when x = 5, y must be 7
We get
7 = 1 x 5 + b
7 = 5 + b
2 = b (subtract 5 from both sides)
b = 2
So the equation of the line is
y = 1x + 2
A line parallel to another line will have the same slope and a different y-intercept
Therefore a parallel line will also have slope 1 and its equation will be of the form
y = 1x + b
To calculate this b, plug in the point (4, 9) into the equation and solve for b
9 = 1 x 4 + b
9 = 4 + b
b = 5
So the equation is
y = 1x + 5
Graph attached shows the real picture