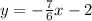Question

Write the equation of a line perpendicular to 6x-7y=-4 that passes through the point (-6,5).

Answer 1

Please read and try to understand it :>

Explanation:

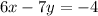`6x-7y=-4` is not the standard format for a straight line so you have to rearrange it:

`y=(6)/(7) x +(4)/(7)`

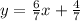
To find the equation of a perpendicular line to the given equation, you have to first find the negative reciprocal of the gradient:

`-(7)/(6)`

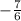
Since you want to find the equation of a perpendicular line that passes a certain point, you have to substitute the coordinates to the equation to find the y-intercept:

`5=-(7)/(6) (-6)+c`

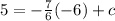
Solving:

`5=-(7)/(6) (-6) +c\\ \\ 5=(42)/(6) +c\\ \\-(42)/(6) +5=c\\ \\-7+5=c\\\\ -2=c`

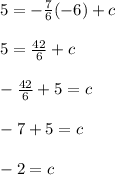
Final equation:
`y=-(7)/(6) x -2`

Answer 2

keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the equation above

`6x-7y=-4\implies 6x=7y-4\implies 6x+4=7y \\\\\\ \cfrac{6x+4}{7}=y\implies \qquad \stackrel{\stackrel{m}{\downarrow }}{\cfrac{6}{7}} x+\cfrac{4}{7}=y\qquad \impliedby \begin{array}c \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}`

now, since we know that slope, let's check for a perpendicular line to it

`\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{\cfrac{6}{7}} ~\hfill \stackrel{reciprocal}{\cfrac{7}{6}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{7}{6}}}`

so we're really looking for the equation of aline whose slope is -7/6 and that it passes through (-6 , 5)

`(\stackrel{x_1}{-6}~,~\stackrel{y_1}{5})\hspace{10em} \stackrel{slope}{m} ~=~ - \cfrac{7}{6} \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{5}=\stackrel{m}{- \cfrac{7}{6}}(x-\stackrel{x_1}{(-6)}) \implies y -5= -\cfrac{7}{6} (x +6) \\\\\\ y-5=-\cfrac{7}{6}x-7\implies {\LARGE \begin{array}{llll} y=-\cfrac{7}{6}x-2 \end{array}}`