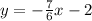Answer:
Please read and try to understand it :>
Explanation:
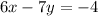 is not the standard format for a straight line so you have to rearrange it:
is not the standard format for a straight line so you have to rearrange it:
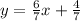
To find the equation of a perpendicular line to the given equation, you have to first find the negative reciprocal of the gradient:
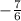
Since you want to find the equation of a perpendicular line that passes a certain point, you have to substitute the coordinates to the equation to find the y-intercept:
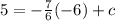
Solving:
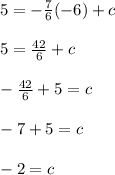
Final equation: