Question

I already found Rx = -0.2 and Ry = -3. The magnitude is the square root of 0.2^2 + 3^2 = 3.01 I only need help understanding why when I plus in to solve for the direction why it won’t accept 86.2 when tan^-1(-3/0.2) doesn’t work. Please help explain to me the real answer or how I’m wrong. Thank you in advance

Answer 1

The values you found are incorrect.

The sum/resultant vector is

`\hat R = \hat A + \hat B \\\\ \hat R = (5.00\,\mathrm m)\,\hat\imath + (6.00\,\mathrm m)\,(-\cos(30.0^\circ)\,\hat\imath - \sin(30.0^\circ)\,\hat\jmath) \\\\ \hat R = (2.00\,\mathrm m) \,\hat\imath - (3\sqrt3\,\mathrm m)\,\hat\jmath \\\\ \hat R \approx \boxed{(2.00\,\mathrm m)\,\hat\imath - (5.20\,\mathrm m)\,\hat\jmath}`

The magnitude of the resultant is

`\|\hat R\| = √((2.00\,\mathrm m)^2 + (-5.20\,\mathrm m)^2) \approx \boxed{5.57\,\mathrm m}`

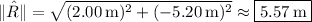
The direction or angle the resultant makes with the positive horizontal axis is
`\theta` such that

`\tan(\theta) \approx (-5.20\,\mathrm m)/(2.00\,\mathrm m) \approx -2.60`

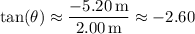
Note the signs of the
`\hat\imath` and
`\hat\jmath` components of
`\hat R`. They tell us that
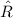`\hat R` points into the fourth quadrant, and this means we can take the inverse tangent of both sides without any extra steps*. We then get

`\theta \approx \tan^(-1)(-2.60) \approx \boxed{-67.0^\circ}`

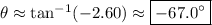
* There would have been an extra step if
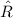`\hat R` were pointing into either the second (negative
`\hat\imath`, positive
`\hat\jmath`) or third quadrant (both negative
`\hat\imath` and
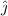`\hat\jmath`). The inverse tangent function has a range of -90° to 90°, which means upon taking the inverse tangent of both sides of

`\tan(\theta) = (R_y)/(R_x) \implies \theta = \tan^(-1)\left((R_y)/(R_x)\right)`

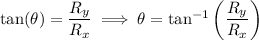
we would only recover some angle
`\theta` between -90° and 90°. Yet our resultant must have some angle between -180° and -90°, or between +90° and +180° to belong to quadrant II or III. To get around this, we add an appropriately chosen multiple of 180° to the right side after taking the inverse tangent.