Question

Using your answer(s) for question 3, were there any extraneous answers, and how did you check?

Question 3 was:
(Solve |2(x-5)|+11=17​)
The answer is x = 8 and x = 2

Answer 1

x = 8 and x = 2 are both valid solutions.

There are no extraneous answers.

Explanation:

Given absolute value function:

`|2(x-5)|+11=17`

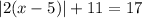
To solve an equation containing an absolute value, isolate the absolute value on one side of the equation:

`\implies |2(x-5)|+11=17`

`\implies |2(x-5)|+11-11=17-11`

`\implies |2(x-5)|=6`

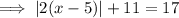
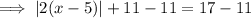
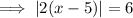
Set the contents of the absolute value equal to both the positive and negative value of the number on the other side of the equation, then solve both equations.

Equation 1 (positive)

`\implies 2(x-5)=6`

`\implies (2(x-5))/(2)=(6)/(2)`

`\implies x-5=3`

`\implies x-5+5=3+5`

`\implies x=8`

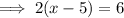
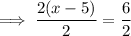
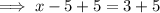
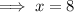
Equation 2 (negative)

`\implies 2(x-5)=-6`

`\implies (2(x-5))/(2)=(-6)/(2)`

`\implies x-5=-3`

`\implies x-5+5=-3+5`

`\implies x=2`

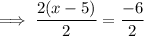
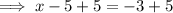
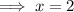
Therefore, the solutions are x = 8 and x = 2.

Check if the solutions are valid by substituting them into the original equation:

`\begin{aligned}x=8 \implies |2(8-5)|+11 & =17\\|2(3)|+11 & =17\\|6|+11 & =17\\6+11 & =17\\ 17 & = 17\end{aligned}`

`\begin{aligned}x=2 \implies |2(2-5)|+11 & =17\\|2(-3)|+11 & =17\\|-6|+11 & =17\\6+11 & =17\\ 17 & = 17\end{aligned}`

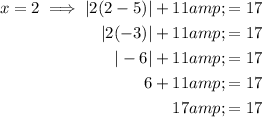
Therefore, both solutions are valid and there are no extraneous answers.

Note: An extraneous solution is a solution that is produced by solving the problem, but is not a valid solution to the problem.