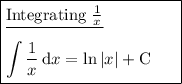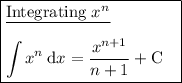Answer:
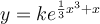
Explanation:
Given differential equation:
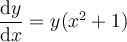
Rearrange the equation so that all the terms containing y are on the left side, and all the terms containing x are on the right side:
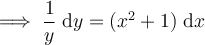
Integrate both sides, remembering to add the constant of integration (C):
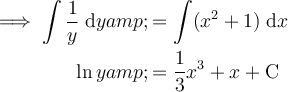
Rewrite C as ln k:
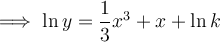
Solve for y, applying:
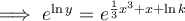
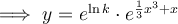
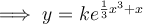
Integration rules