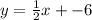Answer:
 or y=1/2x+-6
or y=1/2x+-6
Explanation:
You can use any two points on a line to find slope. For example, I used:
(x1, y1) 2, -5
(x2, y2) 4, -4
To find slope, the following formula is needed:

Input our values:
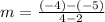 which means m=1/2
which means m=1/2
b is equal to y-intercept which is -6
The equation is: