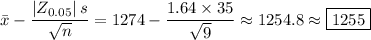Question

Normal Distribution (Standard deviation)
Image attached! Due in 1 hour! please help!

Answer 1

I don't know what kind of calculator you have at your disposal, so I'll just give one way of computing the sample mean and standard deviation.

• To get the mean, add up all the data points and divide the total by the number of data:

`\bar x = \displaystyle \sum_i \frac{x_i}n = \frac{1243+1264+\cdots+1275}9 \approx 1273.89 \\ \implies \boxed{\bar x \approx 1274}`

• To get the s.d. s, first compute the variance s² by adding up the squared difference between each of the data points and the sample mean, and divide the total by 1 less than the number of data:

`s^2 = \displaystyle \sum_i (\left(x_i-\bar x\right)^2)/(n-1) = \frac{(1243-1274)^2+(1264-1274)^2+\cdots+(1275-1274)^2}8 \approx 1211.61`

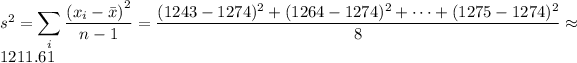
The s.d. is the square root of the variance:

`s^2 \approx 1211.61 \implies s \approx 34.8082 \implies \boxed{s\approx 35}`

The 90% confidence interval for the sample mean has upper and lower limits, respectively, of

`\bar x \pm (\left|Z_(\alpha/2)\right| s)/(\sqrt n)`

(positive root for upper limit, negative root for lower limit)

where
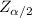`Z_(\alpha/2)` is the critical value for a (1 - α)×100% confidence level. By critical value, I mean

`\mathrm{Pr}\left[ Z \le Z_c \right] = c`

where Z is a random variable following the standard normal distribution.

In this case, we have a 90% confidence level, so α = 0.1, and the critical value is
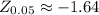`Z_(0.05) \approx -1.64`. Then the confidence interval has upper limit

`\bar x + (\left|Z_(0.05)\right|s)/(\sqrt n) = 1274 + (1.64 * 35)/(\sqrt9) \approx 1292.97 \approx \boxed{1293}`

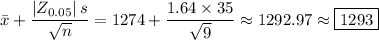
and lower limit

`\bar x - (\left|Z_(0.05)\right|s)/(\sqrt n) = 1274 - (1.64 * 35)/(\sqrt9) \approx 1254.8 \approx \boxed{1255}`