Answer:
62.15 mi/hr
Explanation:
Given:
As both speed limits are given "per hour", we only need to convert 100 km to miles. To do this, set up and solve a ratio for "miles to kilometers", where x is the number of miles to 100 km:
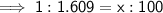
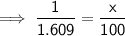
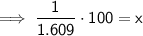
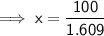
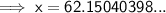
Therefore, 100 km/hr = 62.15 mi/hr (2 d.p.)