First of all, every number in each row is odd, so we can eliminate 392 and 394.
The number of elements in each row forms an arithmetic sequence:
• 1st row : 1 element
• 2nd row : 3 elements - and 3 - 1 = 2
• 3rd row : 5 elements - and 5 - 3 = 2
• 4th row : 7 elements - and 7 - 5 = 2
and so on, so that the
 -th row has
-th row has
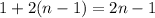 elements.
elements.
This means that in
 complete rows, there is a total of
complete rows, there is a total of
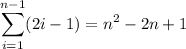
elements, so that the first element in the subsequent
 -th row is the
-th row is the
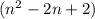 -th number in the sequence {1, 3, 5, 7, …}, i.e the
-th number in the sequence {1, 3, 5, 7, …}, i.e the
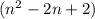 -th odd positive integer. To compute the sum, I use the following well-known formulas.
-th odd positive integer. To compute the sum, I use the following well-known formulas.
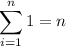
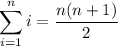
Now, the
 -th term of the sequence {1, 3, 5, 7, …} is simply
-th term of the sequence {1, 3, 5, 7, …} is simply
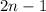 , the
, the
 -th odd positive integer. So the first element in the
-th odd positive integer. So the first element in the
 -th row is
-th row is
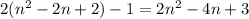
and hence the 1st element of the 15th row is
