Xx^(2)+ 10x =11

Question

X
`x^(2)+ 10x =11`

Answer 1

For this problem, x has multiple values, so we will solve for both.

Explanation:

`x^2+10x-11=11-11\\x^2+10x-11=0\\`

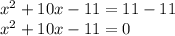
Quadratic rule

`x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

`\mathrm{For\:} a=1,\:b=10,\:c=-11`

`x_(1,\:2)=(-10\pm √(10^2-4\cdot \:1\cdot \left(-11\right)))/(2\cdot \:1)`

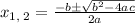
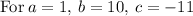
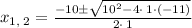
Dealing with radicals

`√(10^2-4\cdot \:1\cdot \left(-11\right))\\=√(10^2+4\cdot \:1\cdot \:11)\\=√(10^2+44)\\=√(100+44)\\=√(144)\\=√(12^2)\\=12\\`

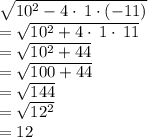
Multi-solution expression

`x_1=(-10+12)/(2\cdot \:1),\:x_2=(-10-12)/(2\cdot \:1)`

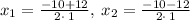
Solve for x₁

`(-10+12)/(2\cdot \:1)\\=(2)/(2\cdot \:1)\\=(2)/(2)\\=1`

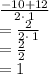
Solve for x₂

`(-10-12)/(2\cdot \:1)\\=(-22)/(2\cdot \:1)\\=(-22)/(2)\\= -(22)/(2)\\= -11`

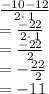
Thus, x has 2 values for 2 different numbers:

x₁ = 1

x₂ = -11

➲ Hope this helps!