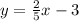Answer:
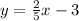
or
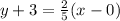
Explanation:
Finding the Equation of a Line Given Two Points:
- In order to find the equation of a line, we must identify point (x,y) and slope (m).
- Slope formula:

- Point-slope formula:

- Slope-intercept formula:

We are given two points on Line A: (0,-3) and (5,-1). We can assign each integer to a variable in the slope formula (see above):
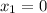
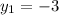
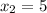
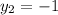
As we have identified point, we can now work to identify slope by substituting our points into the slope formula:
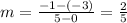
Now that we have identified both point and slope for Line A, we can format these values in point-slope form. Substitute values into the formula:
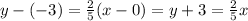
Solve for
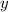 to achieve an answer in slope-intercept form (
to achieve an answer in slope-intercept form (
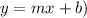 :
: