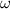 is a 2020th root of unity, so
is a 2020th root of unity, so
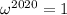 and we have a kind of reflection identity of
and we have a kind of reflection identity of
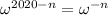 for
for
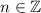 .
.
Let's evaluate the product first. Denote it by
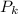 . We split the product where the
. We split the product where the
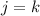 factor would belong, and pull out powers of
factor would belong, and pull out powers of
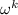 .
.
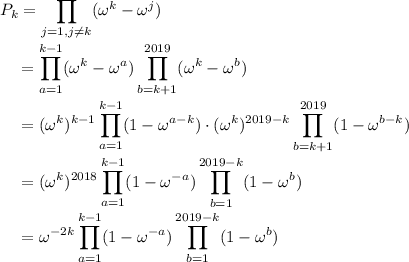
Now introduce some factors to "complete" the
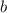 -product and have it contain 2019 factors.
-product and have it contain 2019 factors.
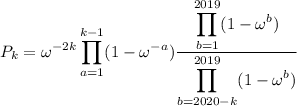
It's relatively straightforward to show that if
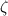 is an
is an
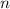 -th root of unity, then
-th root of unity, then
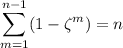
which gives
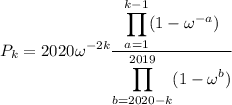
Shifting the index in the denominator and again using the reflection property eliminates all but one factor.
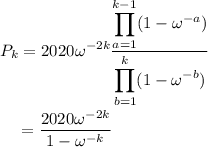
Now evaluate the sum. We can exploit symmetry. Split the sum at the 1010th term, so that
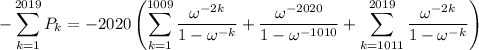
The middle terms reduces to 1/2. Shifting the index in the second sum, we can condense it to
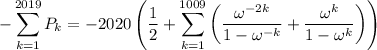
Join the fractions.
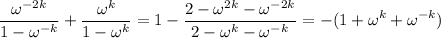
The remaining sums are trivial.
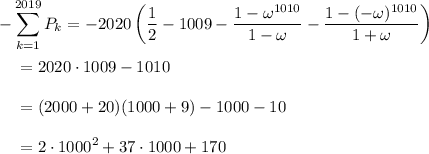
Taking this last result mod 1000, we find the last 3 digits to be 170.