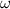Question

`\: \: \: \: \: \: \: \: \: \: \: \: \: \: \:`​

Answer 1

`\omega` is a 2020th root of unity, so
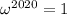`\omega^(2020)=1` and we have a kind of reflection identity of
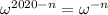`\omega^(2020-n) = \omega^(-n)` for
`n\in\Bbb Z`.

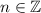Let's evaluate the product first. Denote it by
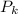`P_k`. We split the product where the
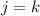`j=k` factor would belong, and pull out powers of
`\omega^k`.

`\displaystyle P_k = \prod_(j=1, j\\eq k) (\omega^k - \omega^j) \\\\ ~~~~ = \prod_(a=1)^(k-1) (\omega^k - \omega^a) \prod_(b=k+1)^(2019) (\omega^k - \omega^b) \\\\ ~~~~ = (\omega^k)^(k-1) \prod_(a=1)^(k-1) (1-\omega^(a-k)) \cdot (\omega^k)^(2019-k) \prod_(b=k+1)^(2019) (1 - \omega^(b-k)) \\\\ ~~~~ = (\omega^k)^(2018) \prod_(a=1)^(k-1) (1 - \omega^(-a)) \prod_(b=1)^(2019-k) (1 - \omega^b) \\\\ ~~~~ = \omega^(-2k) \prod_(a=1)^(k-1) (1-\omega^(-a)) \prod_(b=1)^(2019-k) (1-\omega^b)`

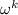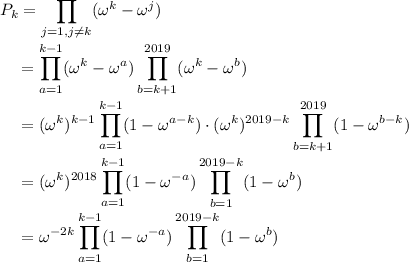
Now introduce some factors to "complete" the
`b`-product and have it contain 2019 factors.

`\displaystyle P_k = \omega^(-2k) \prod_(a=1)^(k-1) (1-\omega^(-a)) (\displaystyle \prod_(b=1)^(2019) (1 - \omega^b))/(\displaystyle \prod_(b=2020-k)^(2019) (1 - \omega^b))`

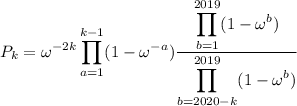
It's relatively straightforward to show that if
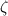`\zeta` is an
`n`-th root of unity, then

`\displaystyle \sum_(m=1)^(n-1) (1-\zeta^m) = n`

which gives

`\displaystyle P_k = 2020 \omega^(-2k) (\displaystyle \prod_(a=1)^(k-1) (1-\omega^(-a)))/(\displaystyle \prod_(b=2020-k)^(2019) (1 - \omega^b))`

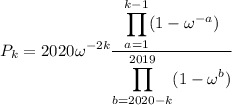
Shifting the index in the denominator and again using the reflection property eliminates all but one factor.

`\displaystyle P_k = 2020 \omega^(-2k) (\displaystyle \prod_(a=1)^(k-1) (1-\omega^(-a)))/(\displaystyle \prod_(b=1)^k (1 - \omega^(-b))) \\\\ ~~~~ = (2020 \omega^(-2k))/(1 - \omega^(-k))`

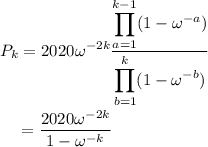
Now evaluate the sum. We can exploit symmetry. Split the sum at the 1010th term, so that

`\displaystyle - \sum_(k=1)^(2019) P_k = -2020 \left(\sum_(k=1)^(1009) (\omega^(-2k))/(1 - \omega^(-k)) + (\omega^(-2020))/(1-\omega^(-1010)) + \sum_(k=1011)^(2019) (\omega^(-2k))/(1-\omega^(-k))\right)`

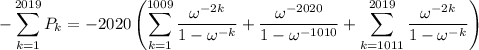
The middle terms reduces to 1/2. Shifting the index in the second sum, we can condense it to

`\displaystyle -\sum_(k=1)^(2019) P_k = -2020 \left(\frac12 + \sum_(k=1)^(1009) \left((\omega^(-2k))/(1-\omega^(-k)) + (\omega^k)/(1-\omega^k)\right)\right)`

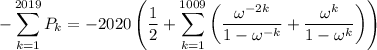
Join the fractions.

`\displaystyle (\omega^(-2k))/(1-\omega^(-k)) + (\omega^k)/(1-\omega^k) = 1 - (2-\omega^(2k)-\omega^(-2k))/(2-\omega^k-\omega^(-k)) = -(1+\omega^k + \omega^(-k))`

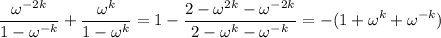
The remaining sums are trivial.

`-\displaystyle \sum_(k=1)^(2019) P_k = -2020 \left(\frac12 - 1009 - (1-\omega^(1010))/(1-\omega) - (1-(-\omega)^(1010))/(1+\omega)\right) \\\\ ~~~~ = 2020\cdot1009 - 1010 \\\\ ~~~~ = (2000+20)(1000+9) - 1000 - 10 \\\\ ~~~~ = 2\cdot1000^2 + 37\cdot1000 + 170`

Taking this last result mod 1000, we find the last 3 digits to be 170.