Answer: 1095
========================================
Step-by-step explanation:
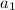 = -10 is the first term
= -10 is the first term
d = 17 is the common difference. We add this amount to each term to get the next one. Eg: -10+17 = 7
We want to find the 66th term, so we'll use n = 66
Plug these values into the nth term arithmetic sequence formula below.

The 66th term is 1095