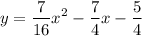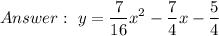
Explanation:
The vertex is also the symmetry point of the parabola. The formula for finding the x-coordinate of the parabola: x = -b/2a (2,-3)
Hence,
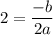
Multiply both parts of the equation by -2a:
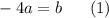
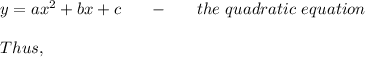
You can make a system of equations on two points belonging to the quadratic equation:
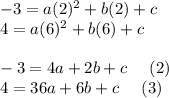
Substitute (1) into equations (2) and (3):
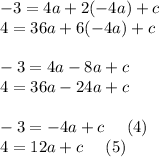
Subtract equation (4) from equation (5):
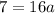
Divide both parts of the equation by 16:
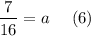
Substitute (6) into equations (1):
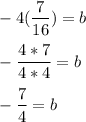
Substitute values a and b into equation (2):
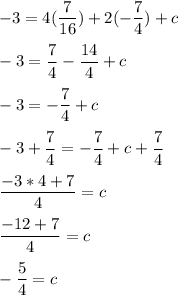
Thus,