Answer:
D. The slingshot reaches a greater height at 150 feet, which is the vertex of the parabola.
Explanation:
First let's examine the given equations
Equation (1) is of the form of a standard equation for a circle
where (a, b) is the center of the circle and r is the radius
Equation (2) is the standard equation of a parabola
y = ax² + bx + c where a, b and c are constant
So we know that the Ferris wheel motion is circular while the slingshot motion is parabolic
Let's compute the highest point at which the Ferris wheel reaches.
Given,
We can see that r² = 5182 by comparing it to the circle equation
Therefore r = √5184 = 72. The diameter = 144 which is the highest point vertically from the center of the circle
The highest point on the circle = 144 + 5= 149 m since there is a 5' gap between the Ferris wheel and the ground at the lowest point so that has to be taken into account
For the parabola the vertex is the highest point and its x-coordinate given by
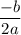 in the standard equation for a parabola
in the standard equation for a parabola
Comparing the given equation with the standard equation we see that a = -4, b = 40 and c= 50
Therefore
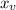 the x-coordinate of the vertex:
the x-coordinate of the vertex:
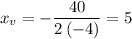
The y coordinate of the vertex can be found by plugging in this value into the parabolic equation
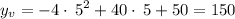
This being the vertical coordinate of vertex of the parabola, the highest point that the slingshot reaches is 150'
So correct answer is D