Answer:
 .
.
.Step-by-step explanation:
The
 -coordinates of the two given points are different. Therefore, the line that goes through these points would not be vertical. Likewise, this line would not be horizontal since the
-coordinates of the two given points are different. Therefore, the line that goes through these points would not be vertical. Likewise, this line would not be horizontal since the
 -coordinates of the given points are different.
-coordinates of the given points are different.
If a line in a plane is of slope
 and goes through point
and goes through point
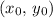 , the point-slope equation of this line would be
, the point-slope equation of this line would be
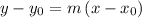 .
.
If a line in a plane goes through the points
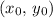 and
and
 (where
(where
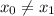 ,) the slope of this line would be
,) the slope of this line would be
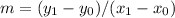 .
.
Since the line in this question goes through points
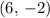 and
and
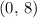 , the slope of this line would be:
, the slope of this line would be:
 .
.
Let
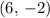 be the point
be the point
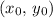 . The point-slope equation of this line would be:
. The point-slope equation of this line would be:
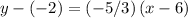 .
.