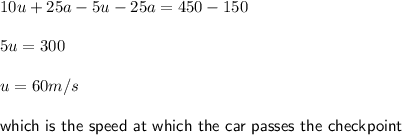Question

A speeding car passes a highway patrol checkpoint, then decelerates at a constant rate. After 5 s, the car is 225 m from the checkpoint, and its speed is then 30 m/s. What was the car’s velocity when it passed the checkpoint?.

Answer 1

Car velocity when crossing checkpoint = 60 m/s

Step-by-step explanation:

For an object traveling at an acceleration of a m/s², with an initial velocity of u m/s the displacement at time = t secs is given in meters by the equation

`\displaystyle d=ut+(1)/(2)at^(2)`

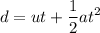
Here we are given displacement, and time but not acceleration and initial velocity : d = 225 meters, t = 5 seconds

Let's find an equation relating u and a in terms of d and using data given

Switching sides we get

`ut+(1)/(2)at^(2)=d`

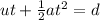
Substituting values for t = 5, d = 225 we get

`5u+(1)/(2)a.25=225`

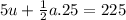
Multiplying both sides by 2 yields

`10u+25a=450\;\;\; ...... (1)`

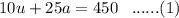
We also have the formula:

`\displaystyle a=\frac{{v-u}}{t}`
where v is the current velocity and u the initial velocity

So

`\displaystyle a=(30-u)/(5)`

`u+5a=30\;\;...... (2)`

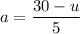
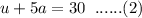
Multiply equation (2) by 5 and subtract from (1) to eliminate the a terms and solve for u

`\displaystyle 10u+25a-5u-25a=450-150\\\\5u=300\\\\u=60m/s\\\\\textsf{which is the speed at which the car passes the checkpoint}\\`