Question

Atlanta's Hartsfield-Jackson International Airport is the busiest airport in the world. On average there are 2,500 arrivals and departures each day.

a. How many airplanes arrive and depart the airport per hour?
b. What is the probability that there are exactly 100 arrivals and departures in one hour?
c. What is the probability that there are at most 100 arrivals and departures in one hour?

Answer 1

Number A is correct.

Explanation:

So, it is asking you what question it is answering.

1. See what it is telling you.

" Atlanta's Hartsfield-Jackson International Airport is the busiest airport in the world. On average there are 2,500 arrivals and departures each day. "

2. Next read the answers.

" a. How many airplanes arrive and depart the airport per hour?

b. What is the probability that there are exactly 100 arrivals and departures in one hour?

c. What is the probability that there are at most 100 arrivals and departures in one hour? "

3. Pick the most reasonable answer.

Now, I might not be right, for I am not a teacher. But this is how I learned how to solve problems like these.

Answer 2

a. On average, around 104.17 airplanes arrive and depart at Hartsfield-Jackson every hour.

b. The probability of exactly 100 arrivals and departures in one hour is around 3.66%.

c. The probability of at most 100 arrivals and departures in one hour is approximately 36.51%.

a. Airplanes per hour:

On average, 2,500 airplanes arrive and depart at Hartsfield-Jackson per day. To find the number per hour, we simply divide by the number of hours in a day:

Airplanes per hour = Total airplanes per day / Hours per day

= 2,500 airplanes / 24 hours

≈ 104.17 airplanes/hour

b. Probability of exactly 100 arrivals and departures:

Assuming arrivals and departures follow independent Poisson distributions (a common model for air traffic), we can calculate the probability of exactly 100 events (arrivals or departures) in one hour using the Poisson probability mass function:

P(X = 100) =
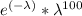`e^((-\lambda)) * \lambda^(100)` / factorial(100)

P(X = 100) is the probability of 100 events

λ is the average number of events per hour (half of the total since we're assuming equal arrivals and departures)

In this case, λ = 104.17 / 2 ≈ 52.085. Plugging this into the formula:

P(X = 100) ≈ 0.0366

c. Probability of at most 100 arrivals and departures:

The probability of at most 100 events, we need to sum the probabilities for all possible event numbers from 0 to 100:

P(X ≤ 100) = Σ P(X = i) for i = 0 to 100

The probability of at most 100 arrivals and departures in one hour is approximately 36.51%.