a. On average, around 104.17 airplanes arrive and depart at Hartsfield-Jackson every hour.
b. The probability of exactly 100 arrivals and departures in one hour is around 3.66%.
c. The probability of at most 100 arrivals and departures in one hour is approximately 36.51%.
a. Airplanes per hour:
On average, 2,500 airplanes arrive and depart at Hartsfield-Jackson per day. To find the number per hour, we simply divide by the number of hours in a day:
Airplanes per hour = Total airplanes per day / Hours per day
= 2,500 airplanes / 24 hours
≈ 104.17 airplanes/hour
b. Probability of exactly 100 arrivals and departures:
Assuming arrivals and departures follow independent Poisson distributions (a common model for air traffic), we can calculate the probability of exactly 100 events (arrivals or departures) in one hour using the Poisson probability mass function:
P(X = 100) =
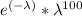 / factorial(100)
/ factorial(100)
P(X = 100) is the probability of 100 events
λ is the average number of events per hour (half of the total since we're assuming equal arrivals and departures)
In this case, λ = 104.17 / 2 ≈ 52.085. Plugging this into the formula:
P(X = 100) ≈ 0.0366
c. Probability of at most 100 arrivals and departures:
The probability of at most 100 events, we need to sum the probabilities for all possible event numbers from 0 to 100:
P(X ≤ 100) = Σ P(X = i) for i = 0 to 100
The probability of at most 100 arrivals and departures in one hour is approximately 36.51%.