Question

Im du.mb at this stuff, i dont know how to do it

Answer 1

the correct answer will be 88

Answer 2

Area of the shaded region 45.76 cm².

Step-by-step Step-by-step explanation:

Firstly, finding the area of rectangle by substituting the values in the formula :

`{\longrightarrow{\pmb{\sf{A_((Rectangle)) = l * b}}}}`

• → A = Area
• → l = length
• → b = breadth

`\begin{gathered} \qquad{\longrightarrow{\sf{A_((Rectangle)) = l * b}}}\\\\\qquad{\longrightarrow{\sf{A_((Rectangle)) = 12* 8}}}\\\\\qquad{\longrightarrow{\sf{A_((Rectangle)) = 96}}}\\\\\qquad{\star{\boxed{\sf{\pink{A_((Rectangle)) = 96 \: {cm}^(2)}}}}} \end{gathered}`

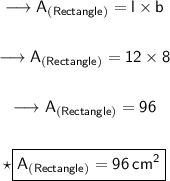
Hence, the area of rectangle is 96 cm².

`\rule{200}2`

Secondly, finding the area of circle by substituting the values in the formula :

`{\longrightarrow{\pmb{\sf{A_((Circle)) = \pi{r}^(2)}}}}`

• → A = Area
• → π = 3.14
• → r = radius

`\begin{gathered} \qquad{\longrightarrow{\sf{A_((Circle)) = \pi{r}^(2)}}} \\ \\ \qquad{\longrightarrow{\sf{A_((Circle)) = 3.14{(4)}^(2)}}} \\ \\ \qquad{\longrightarrow{\sf{A_((Circle)) = 3.14{(4* 4)}}}} \\ \\ \qquad{\longrightarrow{\sf{A_((Circle)) = 3.14(16)}}} \\ \\ \qquad{\longrightarrow{\sf{A_((Circle)) = 3.14 * 16}}} \\ \\ \qquad{\longrightarrow{\sf{A_((Circle)) \approx 50.24}}} \\ \\ \qquad{\star{\boxed{\sf{\purple{A_((Circle)) \approx 50.24 \: {cm}^(2)}}}}} \end{gathered}`

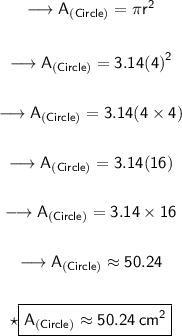
Hence, the area of circle is 50.24 cm².

`\rule{200}2`

Now, finding the area of shaded region by substituting the values in the formula :

`\longrightarrow{\pmb{\sf{A_((Shaded)) = A_((Rectangle)) - A_((Circle))}}}`

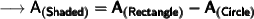
• → A = Area
• → Rectangle
• → Circle

`\begin{gathered}{\quad{\longrightarrow{\sf{A_((Shaded)) = A_((Rectangle)) - A_((Circle))}}}}\\\\{\quad{\longrightarrow{\sf{A_((Shaded)) = 96 - 50.24}}}}\\\\{\quad{\longrightarrow{\sf{A_((Shaded)) \approx 45.76}}}}\\\\{\quad{\star{\boxed{\sf{\red{A_((Shaded)) \approx 45.76 \: {cm}^(2)}}}}}} \end{gathered}`

Hence, the area of shaded region is 45.76 cm².

`\rule{300}{2.5}`