Answer:
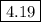 cubic meters.
cubic meters.
Step-by-step Step-by-step explanation:
DIAGRAM :
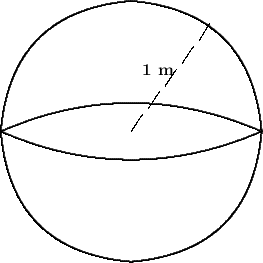

SOLUTION :
Here's the required formula to find the volume of sphere :

- V = Volume
- π = 3.14
- r = radius
Substituting all the given values in the formula to find the volume of sphere :

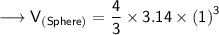
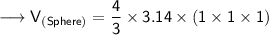
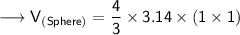
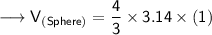
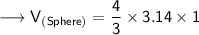
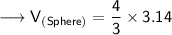


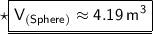
Hence, the volume of sphere is 4.19 m³.

LEARN MORE :

