Question

What is the volume of this sphere?

Use a ~ 3.14 and round your answer to the nearest hundredth.
1 m

Answer 1

volume of this sphere is 4.19 cm³

Step-by-step explanation:

volume of sphere:
`(4)/(3)`πr³

Here the radius of the sphere is 1 meter.

Using the formula:

`(4)/(3)` * 3.14 * 1³

4.19 cm³

Answer 2

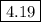`{\purple{\boxed{4.19}}}` cubic meters.

Step-by-step Step-by-step explanation:

DIAGRAM :

`\setlength{\unitlength}{1.2cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\qbezier(-2.3,0)(0,-1)(2.3,0)\qbezier(-2.3,0)(0,1)(2.3,0)\thinlines\qbezier (0,0)(0,0)(0.2,0.3)\qbezier (0.3,0.4)(0.3,0.4)(0.5,0.7)\qbezier (0.6,0.8)(0.6,0.8)(0.8,1.1)\qbezier (0.9,1.2)(0.9,1.2)(1.1,1.5)\qbezier (1.2,1.6)(1.2,1.6)(1.38,1.9)\put(0.2,1){\bf{1\ m}}\end{picture}`

`\begin{gathered}\end{gathered}`

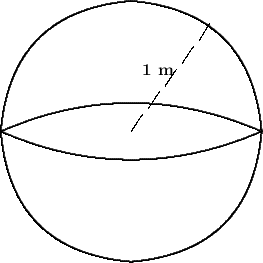
SOLUTION :

Here's the required formula to find the volume of sphere :

`\longrightarrow{\pmb{\sf{V_((Sphere)) = (4)/(3) \pi {r}^(3)}}}`

• V = Volume
• π = 3.14
• r = radius

Substituting all the given values in the formula to find the volume of sphere :

`\longrightarrow{\sf{V_((Sphere)) = (4)/(3) \pi {r}^(3)}}`

`\longrightarrow{\sf{V_((Sphere)) = (4)/(3) * 3.14 * {(1)}^(3)}}`

`{\longrightarrow{\sf{V_((Sphere)) = (4)/(3) * 3.14 * {(1 * 1 * 1)}}}}`

`{\longrightarrow{\sf{V_((Sphere)) = (4)/(3) * 3.14 * {(1 * 1)}}}}`

`{\longrightarrow{\sf{V_((Sphere)) = (4)/(3) * 3.14 * {(1)}}}}`

`{\longrightarrow{\sf{V_((Sphere)) = (4)/(3) * 3.14 * 1}}}`

`{\longrightarrow{\sf{V_((Sphere)) = (4)/(3) * 3.14}}}`

`{\longrightarrow{\sf{V_((Sphere)) = (12.56)/(3)}}}`

`{\longrightarrow{\sf{V_((Sphere)) \approx 4.19}}}`

`\star{\underline{\boxed{\sf{\red{V_((Sphere)) \approx 4.19 \: {m}^(3)}}}}}`

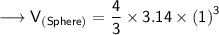
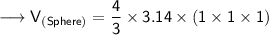
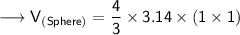
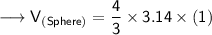
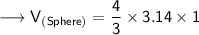
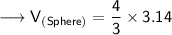
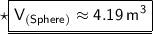
Hence, the volume of sphere is 4.19 m³.

`\begin{gathered}\end{gathered}`

LEARN MORE :

`\begin{array}c\cline{1-3}\bf Shape&\bf Volume\ formula&\bf Surface\ area formula\\\cline{1-3}\sf Cube&\tt l^3}&\tt 6l^2\\\cline{1-3}\sf Cuboid&\tt lbh&\tt 2(lb+bh+lh)\\\cline{1-3}\sf Cylinder&\tt {\pi}r^2h&\tt 2\pi{r}(r+h)\\\cline{1-3}\sf Hollow\ cylinder&\tt \pi{h}(R^2-r^2)&\tt 2\pi{rh}+2\pi{Rh}+2\pi(R^2-r^2)\\\cline{1-3}\sf Cone&\tt 1/3\ \pi{r^2}h&\tt \pi{r}(r+s)\\\cline{1-3}\sf Sphere&\tt 4/3\ \pi{r}^3&\tt 4\pi{r}^2\\\cline{1-3}\sf Hemisphere&\tt 2/3\ \pi{r^3}&\tt 3\pi{r}^2\\\cline{1-3}\end{array}`

`\rule{300}{2.5}`