Answer:
y = -4x - 1
Explanation:
Let's first find the equation of the line segment AB. The equation of a line in slope-intercept form is y = mx + b where m represents the slope and b represents the y-intercept. Start by finding the slope.
Finding the Slope of AB
The equation for slope is:
 . These variables represent any pair of coordinates on the line. In this case since the two points chosen are A and B, thus:
. These variables represent any pair of coordinates on the line. In this case since the two points chosen are A and B, thus:
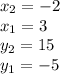
If we plug these values into the equation, we get:
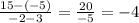
Now we need to find the equation of a line that passes through the point (-1, 3) and is parallel to AB. If two lines are parallel they share the same slope. The equation of the line parallel to AB is y = -4x + b. We can plug in the coordinate (-1, 3) into the equation to solve for b.
Solving for the y-intercept
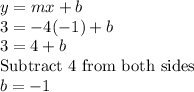
Therefore the equation of the line that passes through the point (-1, 3) and is parallel to AB is y = -4x - 1.