Question

4th term 19 and 7th term is 7 of A5


Find d a1 an a11​

Answer 1

Answer: a₁=31 a₁₁=-9

Explanation:

`\displaystyle\\\left \{ {{a_4=19} \atop {a_7=7}} \right. \\\\a_n=a_1+(n-1)d\\\\\left \{ {{a_1+(4-1)d=19} \atop {a_1+(7-1)d=7}} \right. \\\\\left \{ {{a_1+3d=19\ \ \ \ (1)} \atop {a_1+6d=7\ \ \ \ \ (2)}} \right.`

Subtract equation (2) from equation (1):

`3d=-12`

Divide both parts of the equation by 3:

`d=-4`

Thus,

`a_1+(3)(-4)=19\\a_1-12=19\\a_1-12+12=19+12\\a_1=31\\a_(11)=a_1+(11-1)d\\a_(11)=31+(10)(-4)\\a_(11)=31-40\\a_(11)=-9`

Answer 2

a = 43

d = -6

`\sf a_(11) = -17`

Explanation:

Arithmetic sequence:

Use the formula to find the nth term:

`\sf \boxed{\bf a_n= a+(n-1)d}`

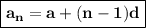
Here, a is the first term, n is the number of terms and d is the common difference.

`\sf a_4 = 19\\\\a+(4-1)*d = 19\\\\a + 3d = 19 -------------------(i)`

`\sf a_7 = 7\\\\a + 6d = 7 ------------------(ii)\\`

Subtract equation (i) from (ii) and thus 'a' will be eliminated and we can find the value of 'd'.

(ii) a + 6d = 7

(i) a + 4d = 19

- - = -

2d = -12

d = -12/2

`\sf \boxed{\bf d = -6}`

Now, plugin d = -6 in any of the two equations. We are substituting the 'd' value in equation (i)

a + 4*(-6) = 19

a - 24 = 19

a = 19 + 24

`\sf \boxed{\bf a = 43}`

`\sf a_(11) = a + 10d`

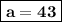
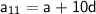
= 43 + 10*(-6)

= 43 - 60

`\sf \boxed{\bf a_(11) = -17 }`