Answer:
a = 43
d = -6

Explanation:
Arithmetic sequence:
Use the formula to find the nth term:
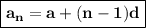
Here, a is the first term, n is the number of terms and d is the common difference.


Subtract equation (i) from (ii) and thus 'a' will be eliminated and we can find the value of 'd'.
(ii) a + 6d = 7
(i) a + 4d = 19
- - = -
2d = -12
d = -12/2

Now, plugin d = -6 in any of the two equations. We are substituting the 'd' value in equation (i)
a + 4*(-6) = 19
a - 24 = 19
a = 19 + 24
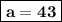
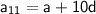
= 43 + 10*(-6)
= 43 - 60
