Question

Find the missing terms in each geometric sequence.

1. 256, ___, ___, -32, -64
2. 27, 9, ___, ___, 1/3
3. 5x^2, ___, 5x^6, 5x^8, ___, ...

Answer 1

1) 256, -128, 64, -32

2) 27, 9, 3, 1, 1/3

3) 5x², 5x⁴, 5x⁶, 5x⁸, 5x¹⁰,

Explanation:

1. In this geometric series each term is obtained by multiplying the previous term by (-1/2) or dividing by (-2).

256 ÷ (-2) = - 128

-128 ÷ (-2) = 64

64 ÷ (-2) = (-32)

The geometric series is:

256, -128, 64, -32...

We can find the common ratio by dividing the second term by first term.

2) 27, 9, ___, _________, 1/3

`\sf \boxed{\bf common \ ratio= (second \ term)/(first \ term)}`

`\sf = (9)/(27)\\\\ = (1)/(3)`

`\sf 9*(1)/(3)=3\\\\3*(1)/(3)=1`

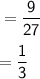
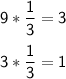
The geometric series is:

27, 9, 3, 1, 1/3....

3) 5x², _____, 5x⁶, 5x⁸, _____, ....

Here, we can take 3rd term and 4th term to find the common ratio.

`\sf common \ ratio = (5x^8)/(5x^6)\\\\`

`\s = x^(8-6)\\\\=x^2`

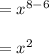
5x² * x² = 5x⁴

8x⁸ * x² = 8x¹⁰

The geometric serious is:

5x², 5x⁴, 5x⁶, 5x⁸, 5x¹⁰, ...

Answer 2

Answer's:

`\sf 1.) \ 256, -128, 64, -32,..\\ \\ 2.) \ 27, 9, 3, 1, 1/3,... \\ \\3.) \ 5x^2, 5x^4, 5x^6, 5x^8,5x^(10) , ...`

`\sf Geometric \ formula: ar^(n-1)`

• where 'a' is first term, 'r' is common ratio.

1)

Find the common ratio:

• next term ÷ previous term

• 32 ÷ -64 = -1/2

Equation:
`256(-(1)/(2) )^(n-1)`

2nd term:
`256(-(1)/(2) )^(2-1)=-128`

3rd term:
`256(-(1)/(2) )^(3-1)=64`

2)

Find common ratio:

• next term ÷ previous term

• 9 ÷ 27 = 1/3

Equation:
`27((1)/(3) )^(n-1)`

3rd term:
`27((1)/(3) )^(3-1)=3`

4th term:
`27((1)/(3) )^(4-1)=1`

3)

Find the common ratio:

• next term ÷ previous term

• 5x^8 ÷ 5x^6 = x^2

Equation:
`5x^2 (x^2)^(n-1)`

2nd term:
`5x^2 (x^2)^(2-1) = 5x^2 (x^2) = 5x^(4)`

5ht term:
`5x^2 (x^2)^(5-1) = 5x^2 (x^8) = 5x^(10)`