Answer:
1) 256, -128, 64, -32
2) 27, 9, 3, 1, 1/3
3) 5x², 5x⁴, 5x⁶, 5x⁸, 5x¹⁰,
Explanation:
1. In this geometric series each term is obtained by multiplying the previous term by (-1/2) or dividing by (-2).
256 ÷ (-2) = - 128
-128 ÷ (-2) = 64
64 ÷ (-2) = (-32)
The geometric series is:
256, -128, 64, -32...
We can find the common ratio by dividing the second term by first term.
2) 27, 9, ___, _________, 1/3
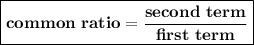
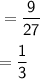
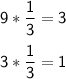
The geometric series is:
27, 9, 3, 1, 1/3....
3) 5x², _____, 5x⁶, 5x⁸, _____, ....
Here, we can take 3rd term and 4th term to find the common ratio.

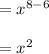
5x² * x² = 5x⁴
8x⁸ * x² = 8x¹⁰
The geometric serious is:
5x², 5x⁴, 5x⁶, 5x⁸, 5x¹⁰, ...