Answer:
The midpoint of the line segment AB
is at (−1, 0).
Explanation:
Midpoint Formula:
In a general sense the midpoint formula for a line segment whose endpoints are
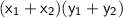
would be the mean of the abscissa and the ordinate as seen in the formula below:
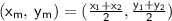
When the line segment lies on one axis, then the there would be only one non-zero value in the ordered pair.
Assuming that the line segment AB
is in the x-axis, then the coordinates of the points would be:
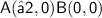
To get the midpoint, substitute the points above in the formula for the midpoint:
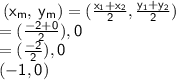
The midpoint of the line segment AB
is at (−1, 0).