Answer:
20
Explanation:
We can solve for the unknown base using Pythagorean's theorem.
Remember Pythagorean's theorem goes as such:

Where a and b are the two legs and c is the hypotenuse. We know one leg and the hypotenuse so we can insert our known values and solve for the unknown.
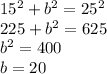
Or using trigonometry:
Note this is a 45-45-90 triangle, therefore all angles are known.
I'll use the sin function with the B angle.

I'm assuming this problem was not made for trig, although the answer is still close.