Question

Can someone please help with this thank u

Answer 1

y = {-1/4 for x < -3; +1/4 for x > -3}

see attached for a graph

Explanation:

You want the function y = |x+3|/(4x+12) written as a piecewise function and graphed.

Absolute value function

The absolute value function resolves into two pieces, each with its own domain. These let you write the function as a piecewise function.

(x+3) < 0

When (x+3) < 0, the absolute value function negates this value:

y = -(x+3)/(4(x+3)) = -1/4 . . . . . for x < -3

(x+3) ≥ 0

When (x+3) ≥ 0, the absolute value function does nothing. That means the equation becomes ...

y = (x +3)/(4(x +3))

When the denominator is zero, the function is undefined. When the denominator is not zero, the function becomes ...

y = 1/4 . . . . . for x > -3

Piecewise function

Then the definition of the piecewise function is ...

`y=\begin{cases}-(1)/(4),&x < -3\\(1)/(4),&x > -3\end{cases}`

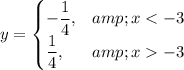
The graph is attached.