Answer:
The pelican was travelling at approximately
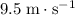 when it dropped the fish.
when it dropped the fish.
The fish hit the water at approximately
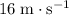 .
.
(Assumption: air resistance on the fish is negligible;
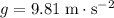 .)
.)
Step-by-step explanation:
During the descent:
- In the horizontal direction, the fish travels at a constant velocity.
- In the vertical direction, the fish accelerates downwards at a constant rate of
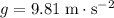 under gravity.
under gravity.
Since acceleration in the vertical direction is constant, make use of the SUVAT equation
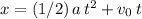 to find the duration
to find the duration
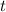 of the descent:
of the descent:
- The vertical position of the fish changed by
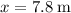 during the entire descent.
during the entire descent. - The vertical acceleration of the fish is
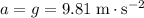
- The pelican was flying horizontally when it dropped the fish. Thus, the initial velocity of the fish in the vertical direction is
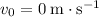 . The equation becomes
. The equation becomes
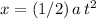 .
.
Rearrange this equation to find the duration of the descent,
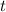 :
:
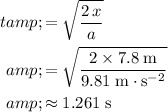 .
.
The vertical speed of the fish right before impact would be:
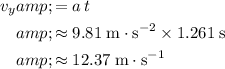 .
.
In the horizontal direction, the speed of the fish was constant- same as the initial speed of the pelican. The fish travelled a horizontal distance of
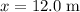 within the
within the
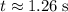 of the descent. As a result, the horizontal velocity of the fish would be:
of the descent. As a result, the horizontal velocity of the fish would be:
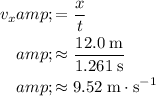 .
.
Hence, the initial speed of the pelican would be approximately
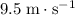 .
.
Thus, right before impact:
- The fish would be travelling at a horizontal velocity of
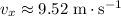 .
. - The fish would be travelling at a vertical velocity of
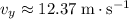 .
.
Apply the Pythagorean Theorem to find the overall velocity of the fish at that moment:
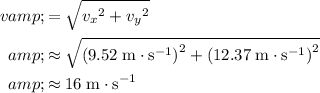 .
.
In other words, the fish would hit the water at approximately
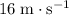 .
.