We can often use Snell's Law to help us find the index of refraction of a refractive medium.
Snell's Law:
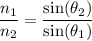
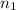 = the refractive index of the first medium
= the refractive index of the first medium
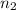 = the refractive index of the second medium
= the refractive index of the second medium
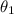 = the angle of incidence
= the angle of incidence
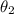 = the angle of refraction
= the angle of refraction
In this question, we're given the following:
- The angle of incidence is
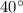 ⇒
⇒

- The first medium is air, which has a refractive index of 1.0003 ⇒
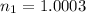
- The angle of refraction is
 ⇒
⇒
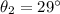
- Solve for
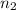 .
.
Since we know we're solving for the index of refraction of the second medium, isolate
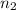 in Snell's Law:
in Snell's Law:

Plug in all the information we know and find
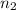 :
:
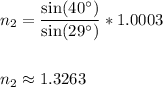
Answer
Therefore, the index of refraction of the refractive medium is approximately 1.3263.