Question

Over the interval 4 ≤ x ≤ 8, does f(x) or g(x)=2x^2+x-1 have a greater average rate of change? Show your work below.

The X coordinates for this interval should be 4, 8 with the y coordinates being 0, 14
I just don't understand what the difference between f(x) and g(x) is supposed to be

Answer 1

Function g(x) has the greater average rate of change over the given interval.

Explanation:

The average rate of change of function f(x) over the interval a ≤ x ≤ b is given by:

`\sf (f(b)-f(a))/(b-a)`

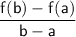
Given:

• f(4) = 0
• f(8) = 14

Therefore, the average rate of change for the function f(x) over the given interval 4 ≤ x ≤ 8 is:

`\sf \implies(f(8)-f(4))/(8-4)=(14-0)/(8-4)=3.5`

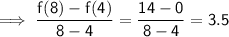
Work out values of function g(x) for x = 4 and x = 8:

`\implies \sf g(4)=2(4)^2+(4)-1=35`

`\implies \sf g(8)=2(8)^2+(8)-1=135`

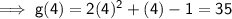
Therefore, the average rate of change for the function g(x) over the given interval 4 ≤ x ≤ 8 is:

`\implies \sf (g(8)-g(4))/(8-4)=(135-35)/(8-4)=(100)/(4)=25`

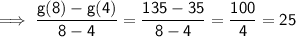
Therefore, function g(x) has the greater average rate of change over the interval 4 ≤ x ≤ 8, as 25 > 3.5.