Answer:
93 square units (the figure is not a rhombus)
Explanation:
You want the area of the figure whose vertex coordinates are A(0,-5), B(9,2), C(12,13), and D(2,7).
Area from coordinates
The formula for the area of a polygon based on its coordinates might be written ...
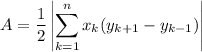
where coordinate indices wrap around from the end to the beginning.
Using this formula, we find the area to be ...
A = 1/2|0(2-7) +9(13-(-5)) +12(7-2) +2(-5-13)|
A = (1/2)|0 +162 +60 -36| = 1/2(186) = 93
The area of the figure is 93 square units.
Diagonals
The area of a rhombus could be calculated as half the product of the lengths of the diagonals. This is only true because the diagonals of a rhombus cross at right angles.
Here, the differences between diagonally opposite coordinates are ...
AC = (12, 18) . . . . slope = 18/12 = 3/2
BD = (-7, 5) . . . . slope = 5/-7 = -5/7
If the diagonals are perpendicular, their slopes have a product of -1. Here, the product is ...
(3/2)(-5/7) = (-15/14) ≠ -1
The given figure is not a rhombus.
If we assume the diagonals are perpendicular, then the area would be ...
A = 1/2√(12²+18²)√((-5)²+7²) = 1/2√34632 ≈ 93.048
Rounded to the nearest tenth, this area would be 93.0 square units.
The diagonals actually cross at an angle of about 88.152°, so the area is actually ...
93.048·sin(88.152°) = 93 square units (exactly)
(Development of this formula is beyond the scope of this answer.)