Answer:
The answer is -3/8.
Explanation:
Hey there!
To find the rate of change, we can use the slope formula.
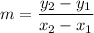
Our values for each are listed below:
- x₁ = 0
- x₂ = 16
- y₁ = 12
- y₂ = 6
Now, we need to do basic arithmetic to find the rate of change by substituting the known values for the coordinates into the slope formula.
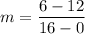
Then, we can simplify by evaluating the numerator and the denominator separately:
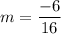
Finally, we can find the simplified version of this fraction:

Therefore, the rate of change is -3/8.