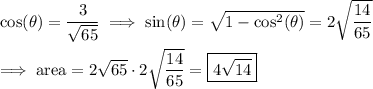Let
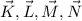 be vectors pointing the vertices K, L, M, and N, respectively.
be vectors pointing the vertices K, L, M, and N, respectively.
The side KL is parallel to and has the same length as the vector
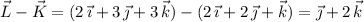
Similarly, the side KN is parallel and as long as
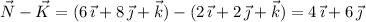
These vectors have magnitudes
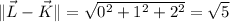
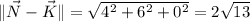
and their dot product is
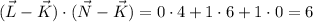
The parallelogram spanned by the vectors
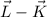 and
and
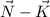 has area equal to the magnitude of their cross product, for which we have the identity
has area equal to the magnitude of their cross product, for which we have the identity
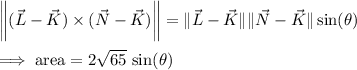
where
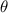 is the angle between the sides KL and KN.
is the angle between the sides KL and KN.
From the dot product identity, we have
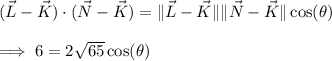
Then