Answer:
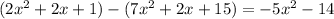
Explanation:
To explain how to approach this question, I am going to place letters in the blank spaces:
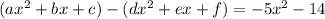
First, compare the coefficients of the x² terms on both sides of the equation:
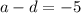
Therefore, we need to choose any two numbers in place of a and d whose difference is -5:
⇒ a = 2 and d = 7 as 2 - 7 = -5.
Similarly, upon comparing the coefficients of the x terms, we can see that there is no x term on the right side of the equation. Therefore, we need to choose numbers in place of b and e for which the difference is zero. So b and e should be the same number:
⇒ b = 2 and e = 2 as 2 - 2 = 0.
Finally, compare the constant term on both sides of the equation:

Therefore, we need to choose any two numbers in place of c and f whose difference is -14:
⇒ c = 1 and f = 15 as 1 - 15 = -14.
Plug in the numbers in place of the letters on the left side of the equation:
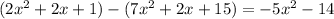
Check
Remove the brackets:
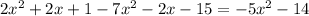
Collect like terms:

Combine like terms:
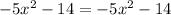
Hence proving that the left and right sides of the equation are the same.