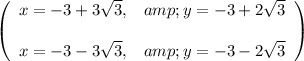Answer
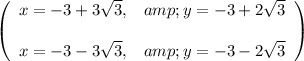
Explanation:
Given system of equations:
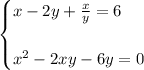
Rearrange the second equation to isolate y:
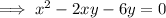
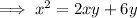
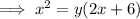
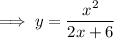
Substitute the found expression for y into the first equation:
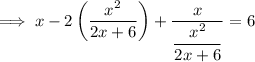
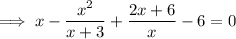
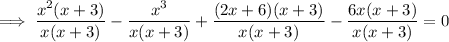
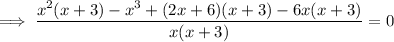
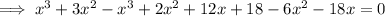
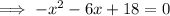
Solve using the Quadratic Formula.
Quadratic Formula
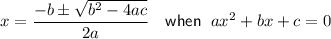
Therefore:
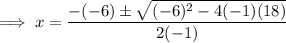
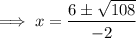
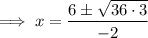
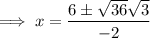
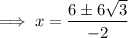
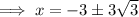
Substitute the found values of x into the expression for y:
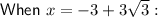
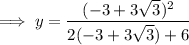
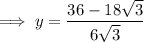
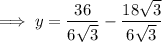
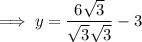
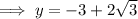
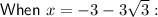
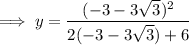
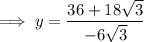
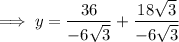
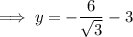
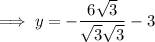
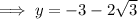
Therefore, the solutions are: