Answer:
88°
Explanation:
the sum of the interior angles of a polygon is
sum = 180° (n - 2 ) ← n is the number of sides
here n = 5 ( sides of a pentagon ) , then
sum = 180° × 3 = 540°
----------------------------------------------------
the angles are in a linear series which means an arithmetic sequence
the sum to n terms of an arithmetic sequence is
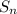 =
=
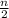 [ 2a₁ + (n - 1)d ]
[ 2a₁ + (n - 1)d ]
where a₁ is the first angle and d the common difference
here d = 10 and S₅ = 540 and a₁ has to be found
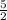 [ 2a₁ + (n - 1)d ] = 540
[ 2a₁ + (n - 1)d ] = 540
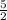 [ 2a₁ + (4 × 10) ] = 540 ( multiply both sides by 2 to clear the fraction )
[ 2a₁ + (4 × 10) ] = 540 ( multiply both sides by 2 to clear the fraction )
5(2a₁ + 40) = 1080 ( divide both sides by 5 )
2a₁ + 40 = 216 ( subtract 40 from both sides )
2a₁ = 176 ( divide both sides by 2 )
a₁ = 88
The smallest angle of the pentagon is 88°