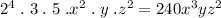Question

Find the least common multiple of 8x³y6z, 6x5z², and
10yzº.

Answer 1

The Least Common Multiple (LCM) of
`8x^3y6z,6x5z^2, \text{ and } 10yz^0 \text{ is } 240 x^3yz^2`

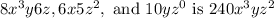
Explanation:

Definition of LCM

The LCM of a, b , c is the smallest multiplier that is divisible by a, b and c

Here the three terms are :

`8x^3y6z`

`6x5z^2`

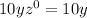`10yz^0=10y` since
`z^0 = 1`

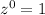
Factoring using prime factorization we get
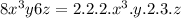`8x^3y6z = 2.2.2.x^3.y.2.3.z`³

=
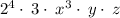`2^4\cdot \:3\cdot \:x^3\cdot \:y\cdot \:z` (1)

Factoring
`6x5z^2` we get

`2\cdot \:3\cdot \:5\cdot \:x\cdot \:z^2` (2)

Factoring
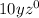`10yz^0` we get

`2 \;\cdot\; 5y` (
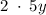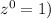`z^0 = 1)` (3)

The LCM is the multiple of each of the highest power in each factor

`2^4\;.\;3\;.\;5\;.x^2\;.\;y\;.z^2 = 240 x^3yz^2`