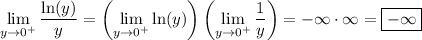Question

\lim {x\to 0}\left(\frac{\ln \left(1 \sqrt{\sin \left(x\right)}\right)}{\sqrt{\tan \left(x\right)}}\right)

Answer 1

It looks like the given limit is

`\displaystyle \lim_(x\to0) (\ln\left(√(\sin(x))\right))/(√(\tan(x)))`

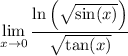
Note that the two-sided limit doesn't exist, since
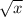`\sqrt x` is defined only for for
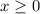`x\ge0`. So I'll further assume you want the one-sided limit as
`x` approaches 0 from above.

`\displaystyle \lim_(x\to0^+) (\ln\left(√(\sin(x))\right))/(√(\tan(x)))`

For
`x` just above zero, we have

`\tan(x) = (\sin(x))/(\cos(x)) = (\sin(x))/(√(1-\sin^2(x)))`

so we can rewrite the limit as

`\displaystyle \lim_(x\to0^+) (√(1-\sin^2(x)) \ln\left(√(\sin(x))\right))/(√(\sin(x)))`

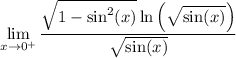
Substitute
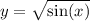`y=√(\sin(x))`. As
`x\to0^+`, so does
`y\to0^+`, and

the limit transforms to

`\displaystyle \lim_(y\to0^+) \frac{√(1-y^4) \ln(y)}y`

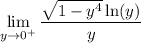
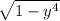`√(1-y^4)` is continuous at
`y=0`, and
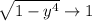`√(1-y^4)\to1`, so we're left with

`\displaystyle \lim_(y\to0^+) \frac{\ln(y)}y = \left(\lim_(y\to0^+) \ln(y)\right) \left(\lim_(y\to0^+) \frac1y\right) = -\infty \cdot \infty = \boxed{-\infty}`